مبانی هوش مصنوعی - الگوریتم های جستجوی محبوب
جستجو، تکنیک جهانی حل مسئله در هوش مصنوعی است. برخی از بازی های تک نفره مانند بازی های رومیزی، سودوکو، جدول کلمات متقاطع و غیره وجود دارند. الگوریتم های جستجو به شما کمک می کنند تا در چنین بازی ها برای یک موقعیت خاص جستجو کنید.
مشکلات مسیریابی عامل واحد
بازی هایی مانند 3X3 هشت تایی، 4X4 پانزده تایی و 5X5 بیست و چهار تایی پازل های تک عامل مسیریابی هستند. آنها از یک ماتریس کاشی با یک کاشی خالی تشکیل شده اند. بازیکن باید کاشی ها را با کشیدن یک کاشی به صورت عمودی یا افقی به یک فضای خالی با هدف انجام برخی از اهداف، مرتب کند.
سایر مثال های مشکلات مسیریابی عامل واحد عبارتند از: مسئله فروشنده دوره گرد، مکعب روبیک و اثبات قضیه.
اصطلاحات جستجوی
-
فضای مسئله − محیطی است که جستجو در آن انجام می شود. (مجموعه ای از حالات و مجموعه ای از عملگرها برای تغییر آن حالات)
-
مورد مسئله − شامل حالت اولیه و حالت هدف است.
-
گرافیک فضای مسئله − نشان دهنده وضعیت مسئله است. حالات با گره ها نشان داده می شوند و عملگرها با لبه ها نشان داده می شوند.
-
عمق یک مسئله − طول کوتاهترین مسیر یا کوتاهترین دنباله ای از عملگرها از حالت اولیه تا حالت هدف است.
-
پیچیدگی فضایی − حداکثر تعداد گره هایی که در حافظه ذخیره می شوند.
-
پیچیدگی زمانی − حداکثر تعداد گره هایی که ایجاد می شوند.
-
قابل قبول بودن − خاصیت یک الگوریتم برای همیشه یافتن یک راه حل بهینه است.
-
عامل شاخه بندی − میانگین تعداد گره های فرزند در گرافیک فضای مسئله.
-
عمق − طول کوتاهترین مسیر از حالت اولیه تا حالت هدف.
استراتژی های جستجوی brute-force
آنها ساده ترین هستند، زیرا به هیچ دانش دامنه خاصی نیاز ندارند. آنها با تعداد کمی از حالات ممکن کار می کنند.
نیازهای −
- توضیحات حالت
- مجموعه ای از عملگرهای معتبر
- حالت اولیه
- توضیحات حالت هدف
جستجوی پهنه ای
از ریشه گره شروع می شود، گره های مجاور را اول بررسی می کند و به سمت گره های مجاور سطح بعدی حرکت می کند. این یک درخت را در هر بار تا زمانی که راه حل پیدا شود، تولید می کند. می توان آن را با استفاده از ساختار داده صف FIFO پیاده سازی کرد. این روش کوتاهترین مسیر را به راه حل ارائه می دهد.
اگر عامل شاخه بندی (تعداد متوسط فرزندان برای یک گره داده شده) = b و عمق = d، پس تعداد گره ها در سطح d = bd است.
کل تعداد گره هایی که در بدترین حالت ایجاد می شوند b + b2 + b3 + … + bd است.
معایب − از آنجایی که هر سطح از گره ها برای ایجاد مرحله بعدی ذخیره می شود، فضای حافظه زیادی را مصرف می کند. فضای مورد نیاز برای ذخیره گره ها نمایی است.
پیچیدگی آن به تعداد گرهها بستگی دارد. میتواند گرههای تکراری را بررسی کند.
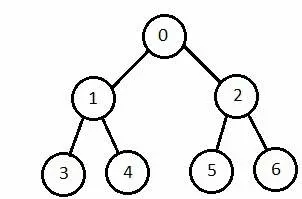
جستجوی عمق-اول
با استفاده از ساختار داده پشته LIFO با بازگشت پیادهسازی میشود. این روش همان مجموعه گرهها را مانند روش Breadth-First ایجاد میکند، فقط به ترتیب متفاوتی.
از آنجایی که گرهها در یک مسیر منفرد در هر تکرار از ریشه تا گره برگ ذخیره میشوند، فضای مورد نیاز برای ذخیره گرهها خطی است. با عامل شاخهای b و عمق به عنوان m، فضای ذخیرهسازی bm است.
معایب − این الگوریتم ممکن است خاتمه نیابد و در یک مسیر به طور نامحدود ادامه دهد. راه حل این مشکل این است که یک عمق برش را انتخاب کنیم. اگر عمق برش ایدهآل d باشد، و اگر عمق برش انتخاب شده کمتر از d باشد، ممکن است این الگوریتم شکست بخورد. اگر عمق برش انتخاب شده بیشتر از d باشد، زمان اجرای آن افزایش مییابد.
پیچیدگی آن به تعداد مسیرها بستگی دارد. نمیتواند گرههای تکراری را بررسی کند.
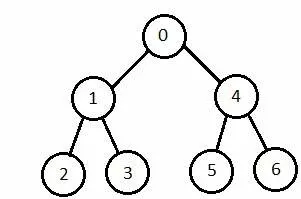
جستجوی دوطرفه
از حالت اولیه به جلو و از حالت هدف به عقب جستجو میکند تا زمانی که هر دو با هم ملاقات کنند و یک حالت مشترک را شناسایی کنند.
مسیر از حالت اولیه با مسیر معکوس از حالت هدف پیوند داده میشود. هر جستجو فقط تا نیمی از مسیر total انجام میشود.
جستجوی هزینه یکنواخت
مرتبسازی بر اساس هزینه increasing مسیر به یک گره انجام میشود. این الگوریتم همیشه گره با کمترین هزینه را گسترش میدهد. این الگوریتم با جستجوی Breadth-First یکسان است اگر هر گذار هزینه یکسانی داشته باشد.
مسیرها را به ترتیب increasing هزینه بررسی میکند.
معایب − ممکن است چندین مسیر طولانی با هزینه <= C* وجود داشته باشد. جستجوی هزینه یکنواخت باید همه آنها را بررسی کند.
جستجوی عمق-اول تعمیق تکراری
جستجوی عمق-اول را تا سطح 1 انجام میدهد، دوباره شروع میکند، یک جستجوی کامل عمق-اول را تا سطح 2 انجام میدهد و به همین ترتیب ادامه میدهد تا زمانی که راه حل پیدا شود.
گرهای ایجاد نمیکند تا زمانی که همه گرههای پایینتر ایجاد شده باشند. فقط یک پشته از گرهها را ذخیره میکند. الگوریتم زمانی به پایان میرسد که یک راه حل در عمق d پیدا کند. تعداد گرههای ایجاد شده در عمق d bd و در عمق d-1 bd-1 است.
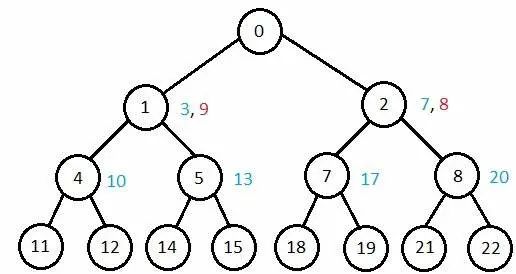
مقایسه پیچیدگی الگوریتمهای مختلف
بیایید عملکرد الگوریتمها را بر اساس معیارهای مختلف ببینیم −
| معیار | جستجوی عرضی | جستجوی عمقی | جستجوی دوطرفه | جستجوی هزینه یکنواخت | جستجوی عمقی تعمیق تکراری |
|---|---|---|---|---|---|
| زمان | bd | bm | bd/2 | bd | bd |
| فضا | bd | bm | bd/2 | bd | bd |
| بهینه بودن | بله | خیر | بله | بله | بله |
| کامل بودن | بله | خیر | بله | بله | بله |
استراتژیهای جستجوی آگاهانه (هوشیار)
برای حل مسائل بزرگ با تعداد زیادی حالت ممکن، باید دانش خاص مسئله را اضافه کرد تا کارایی الگوریتمهای جستجو افزایش یابد.
توابع ارزیابی هیستریک
آنها هزینه مسیر بهینه بین دو حالت را محاسبه میکنند. یک تابع هیستریک برای بازیهای کاشیهای لغزان با شمارش تعداد حرکاتی که هر کاشی از حالت هدف خود انجام میدهد و افزودن این تعداد حرکت برای همه کاشیها محاسبه میشود.
جستجوی هیستریک خالص
گرهها را به ترتیب مقادیر هیستریک آنها گسترش میدهد. دو لیست ایجاد میکند، یک لیست بسته برای گرههای قبلاً گسترش یافته و یک لیست باز برای گرههای ایجاد شده اما گسترش نیافته.
در هر تکرار، یک گره با حداقل مقدار هیستریک گسترش مییابد، همه گرههای فرزند آن ایجاد میشوند و در لیست بسته قرار میگیرند. سپس، تابع هیستریک به گرههای فرزند اعمال میشود و آنها را بر اساس مقدار هیستریک آنها در لیست باز قرار میدهد. مسیرهای کوتاهتر ذخیره میشوند و مسیرهای طولانیتر حذف میشوند.
جستجوی A *
مشهورترین شکل جستجوی بهترین اول است. از گسترش مسیرهایی که قبلاً گران هستند اجتناب میکند، اما اولین مسیرهای امیدوارکننده را گسترش میدهد.
f(n) = g(n) + h(n)، که در آن
- g(n) هزینه (تاکنون) برای رسیدن به گره
- h(n) هزینه تخمینی برای رسیدن از گره به هدف
- f(n) هزینه تخمینی کل مسیر از n به هدف. با افزایش f(n) پیادهسازی شده است.
جستجوی بهترین اول حریصانه
گرهای را که تخمین زده میشود نزدیکترین به هدف است گسترش میدهد. گرهها را بر اساس f(n) = h(n) گسترش میدهد. با استفاده از صف اولویت پیادهسازی شده است.
معایب − ممکن است در حلقهها گیر کند. بهینه نیست.
الگوریتمهای جستجوی محلی
آنها از یک راه حل احتمالی شروع میکنند و سپس به یک راه حل همسایه حرکت میکنند. حتی اگر در هر زمان قبل از پایان کار قطع شوند، میتوانند یک راه حل معتبر برگردانند.
جستجوی صعودی
این یک الگوریتم تکراری است که با یک راه حل دلخواه برای یک مسئله شروع میکند و سعی میکند با تغییر تدریجی یک عنصر از راه حل، یک راه حل بهتر پیدا کند. اگر تغییر، یک راه حل بهتر تولید کند، یک تغییر تدریجی به عنوان یک راه حل جدید گرفته میشود. این فرآیند تا زمانی که بهبودی بیشتر وجود نداشته باشد تکرار میشود.
تابع کوهنوردی (Hill-Climbing)، یک state که یک ماکزیمم محلی است را بازمیگرداند.
inputs: problem, a problem
local variables: current, a node
neighbor, a node
current <-Make_Node(Initial-State[problem])
loop
do neighbor <- a highest_valued successor of current
if Value[neighbor] ≤ Value[current] then
return State[current]
current <- neighbor
end
معایب − این الگوریتم کامل یا بهینه نیست.
جستجوی پرتو محلی
در این الگوریتم، در هر زمان k تعداد حالت وجود دارد. در ابتدا، این حالتها بهصورت تصادفی تولید میشوند. جانشینان این k حالت با کمک تابع هدف محاسبه میشوند. اگر هر یک از این جانشینها حداکثر مقدار تابع هدف باشد، الگوریتم متوقف میشود.
در غیر این صورت، (k حالت اولیه و k تعداد جانشین حالت = 2k) حالت در یک لیست قرار میگیرند. سپس لیست به صورت عددی مرتب میشود. k حالت برتر به عنوان حالتهای اولیه جدید انتخاب میشوند. این فرآیند تا زمانی که مقدار حداکثری حاصل شود ادامه مییابد.
تابع BeamSearch( مشکل، k)، یک حالت راه حل را برمیگرداند.
start with k randomly generated states
loop
generate all successors of all k states
if any of the states = solution, then return the state
else select the k best successors
end
آنیلینگ شبیهسازی شده
آنیلینگ فرایند گرم کردن و سرد کردن یک فلز برای تغییر ساختار داخلی آن و اصلاح خواص فیزیکی آن است. هنگامی که فلز سرد میشود، ساختار جدید آن تثبیت میشود و فلز خواص جدید خود را حفظ میکند. در فرایند آنیلینگ شبیهسازی شده، دما متغیر است.
ما ابتدا دما را بالا میگذاریم و سپس اجازه میدهیم بهتدریج «خنک» شود، زیرا الگوریتم پیش میرود. هنگامی که دما بالا است، الگوریتم مجاز است راهحلهای بدتر را با بسامد بالا قبول کند.
شروع
- k = 0 را مقداردهی اولیه کنید؛ L = عدد صحیح تعداد متغیرها;
- از i -> j، تفاوت عملکرد Δ را جستجو کنید.
- اگر Δ <= 0 باشد، قبول کنید در غیر این صورت اگر exp(-Δ/T(k)) > random(0,1) باشد، قبول کنید;
- مراحل 1 و 2 را برای L(k) مرحله تکرار کنید.
- k = k + 1;
مراحل 1 تا 4 را تا زمانی که معیارها برآورده شوند، تکرار کنید.
پایان
مسئله فروشنده دورهگرد
در این الگوریتم، هدف یافتن یک تور کمهزینه است که از یک شهر شروع میشود، دقیقاً یک بار از همه شهرها در مسیر بازدید میکند و در همان شهر شروع به کار میکند.
Start
Find out all (n -1)! Possible solutions, where n is the total number of cities.
Determine the minimum cost by finding out the cost of each of these (n -1)! solutions.
Finally, keep the one with the minimum cost.
end